Contrastes de hipótesis 👋

Repaso de contrastes de hipóteiss básicos en R

December 15, 2022 9 min read R en Bioestadística

Inferencia

Llegamos a la inferencia en R, aunque no nos vamos a aproximar a la parte teórica. A continuación vamos a repasar de largo una gran porción del vasto de los contrastes estadísticos que tienen su traducción en R.

Base de datos para los ejemplos prácticos

empleados

'data.frame':	474 obs. of  16 variables:
 $ id      : num  1 2 3 4 5 6 7 8 9 10 ...
 $ sexo    : Factor w/ 2 levels "Hombre","Mujer": 1 1 2 2 1 1 1 2 2 2 ...
 $ fechnac : num  1.17e+10 1.19e+10 1.09e+10 1.15e+10 1.17e+10 ...
 $ educ    : num  15 16 12 8 15 15 15 12 15 12 ...
 $ catlab  : Factor w/ 3 levels "Administrativo",..: 3 1 1 1 1 1 1 1 1 1 ...
 $ salario : num  57000 40200 21450 21900 45000 ...
 $ salini  : num  27000 18750 12000 13200 21000 ...
 $ tiempemp: num  98 98 98 98 98 98 98 98 98 98 ...
 $ expprev : num  144 36 381 190 138 67 114 0 115 244 ...
 $ minoría : Factor w/ 2 levels "No","Sí": 1 1 1 1 1 1 1 1 1 1 ...
 $ genero  : Factor w/ 2 levels "Masculino","Femenino": 1 1 2 2 1 1 1 2 2 2 ...
 $ ci      : num  85.7 133.4 122.4 92.6 117.1 ...
 $ edad    : num  38 31.7 60.6 42.9 35 ...
 $ grupedad: Factor w/ 5 levels "Hasta 25 años",..: 4 3 5 5 4 3 3 1 5 5 ...
 $ estudios: Factor w/ 4 levels "Primarios","Secundarios",..: 3 3 2 1 3 3 3 2 3 2 ...
 $ salargr : Factor w/ 4 levels "Hasta 25.000 $",..: 3 2 1 1 2 2 2 1 2 1 ..

Contraste sobre una proporción

Para comparar una proporción observada/muestral contra una proporción teórica.

EJEMPLO: ¿El grosso de mi empresa son administrativos?


addmargins(table(empleados$catlab)) # Cuantos Administrativos hay en mi empresa, sobre el total

# Mi objetivo es saber si la proporción de administrativos sobre el total de mi empresas difiere de 0.5, el valor que marca la mayoría. 

# hO: proporción de administrativos = 0.5

# Contrastes (95%):
binom.test(x= 363,n =474,p = 0.5) # Prueba exacta binomial
prop.test(x= 363,n =474,p = 0.5)  # Contraste sobre una proporción

# Decisión técnica: Se rechaza la hipótesis nula de igualdad (el p valor es < que un alfa de 0.05) 
# Conclusión: La proporción de administrativos en mi empresa es significativamente diferente de 0.5

Contraste sobre una media

Para comparar una media observada/muestral contra una media teórica.

EJEMPLO: ¿Es la media salaria de los administrativos de mi empresa igual que el salario mínimo marcado por el ministerio para dicha categoría (1500 €)? Dato completamente inventado

# ho: La media de salario de los administrativos = 1500
# Supuesto --> Normalidad

shapiro.test(empleados[empleados$catlab == "Administrativo","salario"])

  # La variable no se ajusta a una distribución normal (p-value = 4.568e-16)
  # Sin embargo, como el tamaño muestral es superior a 30, podríamos asumir que la prueba paramétrica es robusta a la ausencia de normalidad 

# Contraste

t.test(empleados[empleados$catlab == "Administrativo","salario"],mu=1500) 
# Decisión técnica: Rechazamos la h0 (pvalor < 0.001)
# Conclusión: El salario de los administrativos de mi empresa difiere significativamente de la media marcada en 1500€


# Opción no paramétrica
wilcox.test(empleados[empleados$catlab == "Administrativo","salario"],mu=1500) # Misma conclusión

Contraste sobre dos proporciones

EJEMPLO: La proporción de mujeres en el grupo de minoría es igual a la de los hombres?

addmargins(table(empleados$sexo,empleados$minoría) )

#          No  Sí Sum
#  Hombre 194  64 258
#  Mujer  176  40 216
#  Sum    370 104 474

# h0: La proporción de hombres/min es la misma que la de mujeres/min

# Contraste
prop.test(x = c(64,40),n = c(258,216)) 

# Decisión técnica: Mantengo la ho (p-value = 0.1245)
# Conclusión: No hay evidencias suficientes para pensar que la proporción de hombres min (0.248) sea diferente de la proporción de mujeres min (0.185)

Test de independencia chi cuadrado

Para comparar las proporciones de manera general en una tabla IxJ (en una tabla 2x2 coincide con prop.test, puedes probarlo con la tabla del apartado anterior). La hipótesis nula comprueba que las dos variables categóricas son independientes (no relación) entre sí.

EJEMPLO: ¿La proporción de mujeres/hombres es igual en todas las categorías laborales?. Es decir, ¿es la categoría laboral independiente del sexo?

t1 <- table(empleados$sexo,empleados$catlab)

#          Administrativo Seguridad Directivo
#  Hombre            157        27        74
#  Mujer             206         0        10

chisq.test(t1)

# Decisión técnica: Rechazo la hipótesis nula de independencia
# Conclusión: Las proporciones son diferentes a nivel general, hay una relación entre el sexo y la categoría laboral. 

# Nota: No estaría recomendado el uso de la chi cuadrado porque el conteo de una celda (Mujer/Seguridad) es 0.

Test exacto de Fisher

El test exacto de Fisher podríamos hacerlo siempre con una tabla 2x2, aunque se suele presentar como alternativa a la chi cuadrado cuando la muestra es pequeña o no se cumplen los supuestos de aplicación.

t2 <- table(empleados$sexo,empleados$minoría)

#h0: La odd ratio verdadera es igual a 1 (No hay relación entre las variables)

fisher.test(t2)

# Decisión técnica: Mantengo la ho (p-value = 0.1186)
# Conclusión: No hay evidencias suficientes para pensar que la proporción de hombres min (0.248) sea diferente de la proporción de mujeres min (0.185)

Odd ratio

Para comprobar la relación entre dos variables categóricas. La odd ratio se suele usar en estudios de prevalencia para observar el efecto de la incidencia de un factor en la presencia de otro.

Siguiendo la formula que presento ahora, es importante asegurarse de mantener la estructura de:

                disease=0   disease=1
exposed=0 (ref)    n00         n01
exposed=1          n10         n11

O de modo equivalente:

               disease=1   disease=0
exposed=1          n11         n10
exposed=0          n01         n00

Ya que así el resultado de la Odd Ratio se podrá interpretar como el peso que tiene el factor de exposición (filas) frente a la incidencia del otro factor (columnas). Sin embargo, existe una argumento para revertir el orden de las columnas, de las filas, o de las dos dimensiones rev=c(“rows”, “columns”, “both”) Hay que elegir solo una entre rows, columns o both.


epitools::oddsratio(t2)

# salida

$data
        
          No  Sí Total
  Hombre 194  64   258
  Mujer  176  40   216
  Total  370 104   474

$measure
        odds ratio with 95% C.I.
          estimate     lower    upper
  Hombre 1.0000000        NA       NA
  Mujer  0.6902863 0.4394743 1.073959

# La Odd Ratio es de 0.69 95%CI[0.439,1.074], por lo que la relación no es significativa, aunque existan más mujeres que no pertenecen al grupo de minoría que hombres, en concreto, la proporción de mujeres que No pertenecen a un grupo de minoritario es 0.67 veces más probable que la proporción de hombres que NO pertenecen a este grupo. 

# Recordad que el 1, en el caso de la Odd Ratio, es el valor que marca la NO relación entre dos factores. 
# Pensad que una ratio es un cociente, y cuando el numerados es igual que el denominador el valor que devuelve el cociente es 1.

Contraste sobre dos medias (Familia t student)

Comparar dos medias de grupos independientes

Ejemplo: ¿La media del salario de las mujeres administrativas es igual a la media de los hombres administrativos?

empleados_administrativos <- empleados[empleados$catlab == "Administrativo",] # La base solo con Administrativos

#ho: La media de salario de las mujeres administrativas = media salario  de los hombres administrativos

# Contraste: Prueba t para muestras independientes

# Supuestos 
  # 1 --> Normalidad
  by(empleados_administrativos$salario, empleados_administrativos$sexo,shapiro.test) # No se cumple la normalidad en ninguno de los dos grupos
  # Sin embargo, el tamaño muestral es grande: Hombres (157), Mujeres (206)
  
  # 2 --> Homogeneidad de varianzas
  bartlett.test(empleados_administrativos$salario~empleados_administrativos$sexo) # No se cumple (p-value = 1.978e-05)
  DescTools::LeveneTest(empleados_administrativos$salario~empleados_administrativos$sexo) # Tampoco con Levene (p=0.021)

  
# Contraste: Prueba t para muestras independientes con varianzas desiguales (t separate)
  
  t.test(empleados_administrativos$salario~empleados_administrativos$sexo,var.equal = F)
  
# Decisión técnica: Rechazo la hipótesis nula (pvalor < 0.001)
# Conclusión: La media de salario de los hombres administrativos (31558.15 €) es significativamente diferente que el de las mujeres administrativas  (25003.69 €)
  
  
# Contraste SI SE HUBIESE CUMPLIDO LA IGUALDAD DE VARIANZAS  
  
  t.test(empleados_administrativos$salario~empleados_administrativos$sexo,var.equal = T)
  
# Alternativa NO PARAMÉTRICA 
  
  wilcox.test(empleados_administrativos$salario~empleados_administrativos$sexo)

Comparar dos medias emparejadas (dos variables contínuas)

EJEMPLO: ¿Ha existido una mejora significativa entre el salario inicial de los empleados y el actual?


#ho: salario_actual - salario_inicial = 0
#o : media salario actual = media salario inicial

# Opción 1: Contraste sobre una media

dif <- empleados$salario - empleados$salini # Creo la variable de la diferencia

t.test(dif,mu = 0) # t = 35.036, df = 473, p-value < 2.2e-16

# Opción 2: Contraste sobre dos medias emparejadas

t.test(empleados$salario, empleados$salini,paired = T) #t = 35.036, df = 473, p-value < 2.2e-16


# Decisión técnica: Rechazo la hipótesis nula
# Conclusión: Ha habido una mejora general del salario inicial, en concreto, una media de 17403.48 €

Comparación de más de dos medias

ANOVA de un factor

EJEMPLO: ¿Existen diferencias en el salario en función de la categoría laboral?


# ho: La media en el salario en función de la categoría laboral no difieren: u1 = u2 = u3

# Supuestos: 
  # 1 Normalidad
  by(empleados$salario,empleados$catlab,shapiro.test) # No se cumple normalidad en ningún grupo

  # 2 Homoceasticidad
  
  bartlett.test(empleados$salario ~empleados$catlab) # No hay homoceasticidad (pvalor < 0.001)
  
  # Técnicamente no podríamos continuar con el ANOVA. No se cumple la normalidad en todos los grupos, el tamaño muestral del grupo de seguridad es n=27, y no se cumple el supuesto de homoceasticidad. Pero para el ejercicio vamos a ignorar estas violaciones. 

  
# CONTRASTE: ANOVA
res_anova <- aov(empleados$salario ~empleados$catlab)
summary(res_anova) # tabla de anova


# salida 
                  Df    Sum Sq   Mean Sq F value Pr(>F)    
empleados$catlab   2 8.944e+10 4.472e+10   434.5 <2e-16 ***
Residuals        471 4.848e+10 1.029e+08                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1


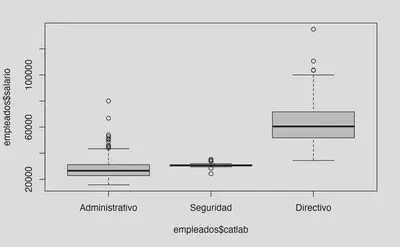
boxplot(empleados$salario ~empleados$catlab) # Vemos gráficamente las diferencias


# Decisión técnica: Rechazamos la hipótesis nula de igualdad de medias (pvalor < 0.001)
# Conclusión: Las medias son desiguales de manera general. En el gráfico se puede ver que la media de los directivos es sustancialmente mayor. Faltaría ver con comparaciones post-hoc las comparaciones por pares, es decir, ver la significación de todas las combinaciones entre los grupos: administrativo vs seguridad, administrativo vs directivo y seguridad vs directivo

# post hoc

TukeyHSD(res_anova) 


# salida
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = empleados$salario ~ empleados$catlab)

$`empleados$catlab`
                              diff       lwr       upr     p adj
Seguridad-Administrativo  3100.349 -1657.805  7858.503 0.2768689
Directivo-Administrativo 36139.258 33251.225 39027.291 0.0000000
Directivo-Seguridad      33038.909 27761.979 38315.839 0.0000000


# La diferencia entre seguridad y administrativa no es significativa (p = 0.2768689), pero el salario medio de los directivos es significativamente mayor que los grupos de administrativos  (p < 0.001) y seguridad  (p < 0.001)

# Alternativa no paramétrica

kruskal.test(empleados$salario ~empleados$catlab) # Llegamos a la misma conclusión que el ANOVA.

inferencia contrastes medias proporciones