Descriptivos desagregados, tablas y gráficos 👋

Descriptivos

Desgragegando por una variable categórica

Recordemos que anteriormente hemos visto varios paquetes para calcular los descriptivos de una tacada. Hemos repasado principalmente las funciones psych::describe(), skimr::skim(), Hmisc::describe() .

# Descriptivos generales
psych::describe(exams)

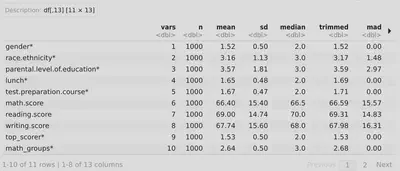
Sin embargo, muchas veces nos interesa calcular desagregando los descriptivos en función de alguna variable de interés. El modo rudimentario para calcular los descriptivos en cada grupo de una variable categórica sería filtrar la base de datos para cada uno de los valores distintos de la variable en cuestión (e.g., filtrar por “male” y “female”) y calcular dos veces los descriptivos. Sin embargo, en R existe una función genérica que permite aplicar otras funciones por grupos marcados por una variable. Esta función es by()

by()

Esta función es muy útil para incorporarlas dentro de analisis desagregados. A menudo nos encontraremos utilizando esta función para calcular los descriptivos en función de alguna variable categórica o para sacar un histogragama para cada grupo sobre una variable, o incluso para aplicar contrastes de normalidad divididos por grupos.

# Función general by ()

by(data = , # Variable dependiente o variable sobre la que se aplicará la función pasada en el argumento FUN
   INDICES = , # Variable independiente o variable que incluya los grupos por lo que se desagregará la función 
   FUN =) # Función que se quiera aplicar a cada uno de los grupos que marque INDICES sobre data. 


by(data = exams$math.score,
   INDICES = exams$lunch,
   FUN = psych::describe) #Output: Dos tablas de descriptivos. Una por cada grupo de la variable pasada en INDICES.

# psych::describe tiene una función donde incorpora el by
psych::describe.by(exams$reading.score,group = exams$gender) #by incorporado en psych; mismo resultado


### Output

 Descriptive statistics by group 
group: female
   vars   n  mean    sd median trimmed   mad min max range  skew kurtosis
X1    1 483 71.89 14.66     72   72.21 14.83  29 100    71 -0.21    -0.31
     se
X1 0.67
---------------------------------------------------------- 
group: male
   vars   n  mean    sd median trimmed   mad min max range  skew kurtosis
X1    1 517 66.31 14.31     67   66.67 14.83  27 100    73 -0.22    -0.34
     se
X1 0.63

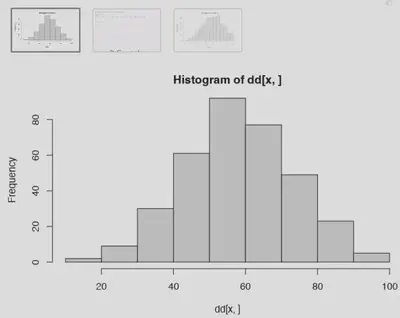
# Otros ejemplos con by
by(data = exams$math.score,
   INDICES = exams$lunch,
   FUN = hist) # Output: Dos gráficos. Uno por cada grupo de la variable pasada en INDICES 

Gráficos principales

Histograma

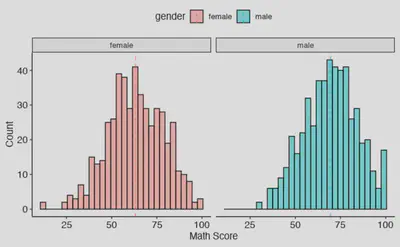
Como acabamos de ver en el ejemplo de by(), uno de los gráficos más útiles para formarse una idea sobre una variable cuantitativa es un histograma. Con by podemos graficar el histograma una variable cuantitativa en cada grupo de otra variable categórica, pero también lo podemos incluir en el parámetro de facet.by de gghistogram()

hist(exams$math.score) # básico

##### Avanzado

ggpubr::gghistogram(data = exams,
                    x = "math.score",    # Variable en eje x
                    fill = "gray23",     # Color de relleno de las barras / color por variable
                    add = "mean",        # Añadir línea con media
                    xlab = "Math Score", # Cambiar etiqueta eje x
                    ylab = "Count",      # Cambiar etiqueta eje y
                    facet.by = "gender") + # Dividir en paneles por variable categórica     
                                          # + Añadir otros elementos /configuraciones al gráfico
  ggpubr::theme_pubr()                   # Función que incluye la configuración de un "tema" 

Boxplot

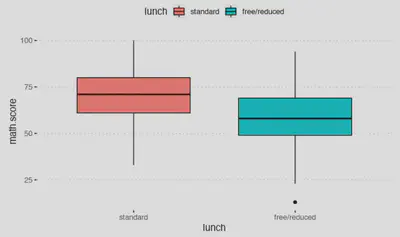
Para dibujar una variable cuantitativa en función de una variable categórica la mejor opción es un diagrama de cajas.

Atención, pregunta de exámen: el descriptivo de centralidad representado como una línea horizontal dentro de las cajas es la mediana, NO la media.

boxplot(exams$math.score ~ exams$lunch) # variable dependiente en función (~) de variable independiente

##### Avanzado

ggpubr::ggboxplot(data = exams,
                  x = "lunch",
                  y = "math.score",
                  fill = "lunch",    # Podemos rellenar las cajas en función de una variable
                  ggtheme  = ggpubr::theme_pubclean()  
                  ) 

Densidad

ggpubr::ggdensity(data = exams,
                  x = "math.score",
                  fill = "gray",
                  ggtheme  = ggpubr::theme_pubr() )

Tabla de contingencia

table()

Hasta ahora hemos avanzando solo con los descriptivos generales, sin embargo, hemos saltado un modo imprescindible de observar las variables categóricas: las tablas de contigencia.

En las tablas de contigencia están representados los conteos (frecuencias absolutas) de cada categoría de una variable. Pueden incluir una variable, pero lo más común es mostrar dos variables dentro de la tabla.

La creación de una tabla de contigencia es el primer paso para observar la relación entre dos variables categóricas.

table(exams$lunch) # De una sola variable
table(exams$lunch, exams$race.ethnicity) # Con dos variables 
#table(exams$lunch, exams$race.ethnicity, exams$gender) # Se podría incluso con tres variables. La ultima variable sería la que forma la categoria superior. 

### output

          
               group A group B group C group D group E
  free/reduced      26      70     115      78      59
  standard          53     135     208     184      72

La tabla toma la forma de i*j donde i son las categorías de la primera variable, y j las categorías de la segunda variable. Un modo para observar además los totales marginales en cada grupo (filas, columnas y total) podemos aplicar la función addmargins()

t1 <- table(exams$lunch, exams$race.ethnicity) # Tabla 2*5 anterior. La guardamos como t1

addmargins(t1)

### output 

             group A group B group C group D group E  Sum
  free/reduced      26      70     115      78      59  348
  standard          53     135     208     184      72  652
  Sum               79     205     323     262     131 1000

Tabla de proporciones

prop.table()

Después de crear una tabla de contigencia, podemos estar interesados en sacar una tabla de proporciones. Técnicamente este paso de crear la tabla de frecuencias relativas es muy fácil: Bastaría con aplicar la función prop.table() Sin embargo, este proceso requiere una complejidad adicional que no tiene nada que ver con el código o su mismo proceso.

Dentro de una tabla de proporciones podemos marcar la dirección de la proporción en función de los totales marginales (filas o columnas) o del total absoluto. De este modo, si nos limitamos a aplicar la función sobre una tabla, la proporción de cada celda será calculada sobre el total absoluto de observaciones. En el ejemplo, podemos ver como la primera proporción (0.026) es el resultado de dividir 26, el conteo del cruce entre free/reduced y el grupo A, entre 1000, el total de alumnos incluidos en la muestra.

prop.table(t1) # sin especificar ninguna dirección, las proporciones se calculan sobre el total. 
              group A group B group C group D group E     
  free/reduced   0.026   0.070   0.115   0.078   0.059
  standard       0.053   0.135   0.208   0.184   0.072 

  

Sin embargo, la mayoría de las veces nos interesa ver las proporciones en función de una variable específica. Para ello, debemos especificar en el argumento margin la dirección que queremos dar a la proporción. ¿Donde está la complejidad en esto? La dificultad reside interpretar bien la dirección que nos interesa para ajustarnos a la pregunta que intentamos resolver con los análisis. Al encarar estos problemas tenemos que pensar que variable impone el total en la proporción pues será la que marque el denominador y dirección en la proporción. En la tabla de ejemplo no es lo mismo querer ver el reparto de los grupos étnicos en cada una de las modalides de comedor, que preguntarse cuál es la proporción de la modalidad de comedor dentro de cada grupo étnico. En el primer caso la proporción está en función de la variable “lunch” y en el segundo caso es la variable “ethnicity” la que marca la dirección.

Una vez que sepamos que variable marca la dirección tenemos que observar en que posición de la tabla la hemos situado. Si nuestra variable está en las filas la dirección que debemos imponer en el argumento margin será 1, si por el contrario está en las columnas será la dirección 2.

# Es importante especificar bien la dirección de la proporción. 1 = filas, 2 = columnas
# La dirección la impondrá la variable independiente. 


# Modalidad comedor EN FUNCIÓN de grupo étnico
prop.table(t1,margin = 2) # Dentro de cada grupo formado por la variable de las columnas, cual es el reparto de la var de las filas

              
                 group A   group B   group C   group D   group E
  free/reduced 0.3291139 0.3414634 0.3560372 0.2977099 0.4503817
  standard     0.6708861 0.6585366 0.6439628 0.7022901 0.5496183

# Grupo étnico EN FUNCIÓN de la modalidad de comedor
prop.table(t1,margin = 1) # Dentro de cada grupo formado por la variable de las filas, el reparto de las var de las columnas


                 group A    group B    group C    group D    group E
  free/reduced 0.07471264 0.20114943 0.33045977 0.22413793 0.16954023
  standard     0.08128834 0.20705521 0.31901840 0.28220859 0.11042945