Ejercicio de Descriptivos / Inferencia I 👋
Ejercicio para practicar examen de bioestadística en R
Base de datos
Base de datos extraída de “Análisis de datos en ciencias sociales y de la salud” https://www.sintesis.com/metodologia-de-las-ciencias-del-comportamiento-y-de-la-salud-22/analisis-de-datos-en-ciencias-sociales-y-de-la-salud-i-ebook-1525.html
str(empleados)
'data.frame': 474 obs. of 16 variables:
$ id : num 1 2 3 4 5 6 7 8 9 10 ...
$ sexo : Factor w/ 2 levels "Hombre","Mujer": 1 1 2 2 1 1 1 2 2 2 ...
$ fechnac : num 1.17e+10 1.19e+10 1.09e+10 1.15e+10 1.17e+10 ...
$ educ : num 15 16 12 8 15 15 15 12 15 12 ...
$ catlab : Factor w/ 3 levels "Administrativo",..: 3 1 1 1 1 1 1 1 1 1 ...
$ salario : num 57000 40200 21450 21900 45000 ...
$ salini : num 27000 18750 12000 13200 21000 ...
$ tiempemp: num 98 98 98 98 98 98 98 98 98 98 ...
$ expprev : num 144 36 381 190 138 67 114 0 115 244 ...
$ minoría : Factor w/ 2 levels "No","Sí": 1 1 1 1 1 1 1 1 1 1 ...
$ genero : Factor w/ 2 levels "Masculino","Femenino": 1 1 2 2 1 1 1 2 2 2 ...
$ ci : num 85.7 133.4 122.4 92.6 117.1 ...
$ edad : num 38 31.7 60.6 42.9 35 ...
$ grupedad: Factor w/ 5 levels "Hasta 25 años",..: 4 3 5 5 4 3 3 1 5 5 ...
$ estudios: Factor w/ 4 levels "Primarios","Secundarios",..: 3 3 2 1 3 3 3 2 3 2 ...
$ salargr : Factor w/ 4 levels "Hasta 25.000 $",..: 3 2 1 1 2 2 2 1 2 1 ...
PREGUNTAS
1. Calcula los descriptivos y comenta brevemente la variable salario en función del sexo
by(empleados$salario,
empleados$sexo,
psych::describe)
##################
# empleados$sexo: Hombre
# vars n mean sd median trimmed mad min max range skew kurtosis se
# X1 1 258 41441.78 19499.21 32850 38256.15 9785.16 19650 135000 115350 1.62 2.66 1213.97
# --------------------------------------------------------------------------
# empleados$sexo: Mujer
# vars n mean sd median trimmed mad min max range skew kurtosis se
# X1 1 216 26031.92 7558.02 24300 25012.76 5114.97 15750 58125 42375 1.84 4.44 514.26
##################
R: Los tamaños muestrales son muy parecidos, sin embargo, en el grupo de los hombres tanto la media como la desviación son muy superiores al de las mujeres. Los hombres tienen una media de 41,441 € y las mujeres casi la mitad (26,031€)
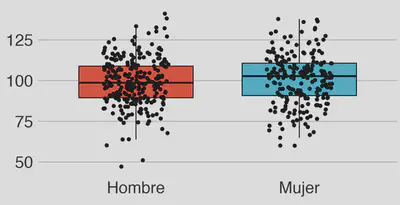
2. Dibuja el diagrama de cajas de la variable ci (inteligencia) en función del sexo.
boxplot(empleados$ci~empleados$sexo)
##################
# boxplot avanzado
ggpubr::ggboxplot(empleados,
x = "sexo",
y = "ci",
add = "jitter",
fill = "sexo",
palette = "npg") +
bbplot::bbc_style()
R: La mediana del CI del grupo de mujeres es superior a la de los hombres
3. Desde hace tiempo se conoce que la distribución del CI se distribuye de manera normal con media 100 y desviación típica 15.
Responde si en nuestra muestra
a) Se distribuye de manera normal
# normalidad
shapiro.test(empleados$ci)
#######
# Shapiro-Wilk normality test
#
#data: empleados$ci
#W = 0.99692, p-value = 0.5124
######
Ra: Podemos asumir la normalidad de la variable dado que mantenemos la h0 de igualdad de centros en las distribuciones normal y muestral (0.51>0.005)
b) La media es diferente a la esperada
# Contraste sobre una media
# Ho: La media muestral es igual a 100
#Supuestos ---> hemos comprobado normalidad
t.test(empleados$ci,mu=100)
# One Sample t-test
#
# data: empleados$ci
# t = 0.093986, df = 473, p-value = 0.9252
# alternative hypothesis: true mean is not equal to 100
# 95 percent confidence interval:
# 98.69996 101.43065
# sample estimates:
# mean of x
# 100.0653
Rb: Decisión. Como el pvalor es superior al alpha (0.05), mantenemos la hipotesis nula, y concluimos que no hay evidencias suficientes para pensar que la media muestral es distinta a la esperada (media ci = 100)
4. En la empresa están preocupados por la discriminación laboral. Según el estado, la proporción de mujeres directivas de una empresa que cumple con los estandars de género debe ser del 0.5. ¿Tienen razón a estar preocupados en la empresa?
El criterio es inventado
t1 <- table(empleados$sexo,empleados$catlab)
addmargins(t1)
# Administrativo Seguridad Directivo Sum
# Hombre 157 27 74 258
# Mujer 206 0 10 216
# Sum 363 27 84 474
prop.test(10,84,0.5)
# El pvalor (6.249e-12) es inferior a alpha (0.05), por lo que rechazamos la ho de igualdad de proporciones y asumimos que hay diff significativas.
R: La proporción de mujeres directivas en la empresa es 0.12, significativamente diferente al criterio que marca el estado (0.5)
5. La empresa afirma que hay una mejora general en el salario inicial, y el actual. ¿Es verdad?
# H0: La media del salario actual es igual a la media del salario inicial
# Supuestos
# Normalidad de la diferencia?
shapiro.test(empleados$salario-empleados$salini) # No se cumple la normalidad
# PERO, el tamaño muestral es grande (n = 474) podemos asumir que la prueba t será robusta a la ausencia de normalidad
# Prueba paramétrica (por tamaño muestral)
t.test(empleados$salario,empleados$salini,paired = T)
# Paired t-test
#
# data: empleados$salario and empleados$salini
# t = 35.036, df = 473, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 16427.41 18379.56
# sample estimates:
# mean of the differences
# 17403.48
# Alternativa como si fuese contraste sobre una media
t.test (empleados$salario-empleados$salini,mu = 0)
# Prueba no paramétrica ()
wilcox.test(empleados$salario,empleados$salini,paired = T)
# Decisión
# Rechazamos la h0 de igualdad, y podemos concluir que sí hay una mejora general en el salario.
R: Hay una mejora media de 17,403 €
6. Hay diferencias en esa mejora en función del sexo?
dif_salario <- empleados$salario - empleados$salini
# Supuestos
# Normalidad ... Lo resolvemos por el tamaño muestral (n = 474)
# Homoceasticidad
DescTools::LeveneTest(dif_salario ~ empleados$sexo) # Rechazamos la h0, no podemos asumir igualdad de varianzas en los grupos
# Levene's Test for Homogeneity of Variance (center = median)
# Df F value Pr(>F)
# group 1 40.03 5.816e-10 ***
# 472
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# Prueba
#HO: La mejora del salario es la misma en los grupos de hombres y mujeres
t.test(dif_salario ~ empleados$sexo,var.equal=F)
# Welch Two Sample t-test
# data: dif_salario by empleados$sexo
# t = 9.4094, df = 370.81, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 6486.710 9914.158
# sample estimates:
# mean in group Hombre mean in group Mujer
# 21140.39 12939.95
# Decisión:
# Rechazo Ho de igualdad de medias (p<alpha)
R: La mejora salarial es superior en el grupo de los hombres (21,140 €) respecto las mujeres (12,939 €)
Adrián Muñoz García
Data Scientist and Statistics Professor
My research interests are Behavioral Economics, Cognition and Methods